Prove that:
cot π/20 . Cot 3π/20 . Cot 5π/20 . Cot 7π/20 . Cot9π/20 = 1
We use the value: $π^c$ = 180°
Answer:
Taking LHS
= cot $\frac{π^c}{20}$ .cot $\frac{3π^c}{20}$ .cot$\frac{5π^c}{20}$ .cot
$\frac{7π^c}{20}$ .cot $\frac{9π^c}{20}$
= cot $\frac{π^c}{20}$ .cot $\frac{3π^c}{20}$ .cot$\frac{5π^c}{20}$ .cot
$\left ( \frac{π^c}{2} -\frac{3π^c}{20} \right)$ .cot $\left (
\frac{π^c}{2} -\frac{π^c}{20} \right)$
= cot $\frac{π^c}{20}$ .cot $\frac{3π^c}{20}$ .cot$\frac{5π^c}{20}$
.tan $\frac{3π^c}{20}$ .tan $\frac{π^c}{20}$
= cot $\frac{π^c}{20}$ .tan $\frac{π^c}{20}$ .cot$\frac{3π^c}{20}$
.tan $\frac{3π^c}{20}$ .cot $\frac{5π^c}{20}$
= 1 * 1 * cot $\frac{5π^c}{20}$
= cot $\dfrac{5*180°}{20}$
= cot 45°
= 1
= RHS
I won't explain the answer but rather show you the values of them.
Once you put the value of sin and cos as indicated in the question and
perform the basic Mathematics, you will get your answer.
Advertisement

Also, you need to understand these formulas (a part of CAST formula)
You need to understand the above-mentioned values of Trigonometric ratios
at different angles to be able to solve such questions.
Related solutions:
- Prove that: cos²(7π/8) + cos²(5π/8) + cos²(3π/8) + cos²(π/8) = 2
- Prove that: cos(π/8) + cos(3π/8) + cos(5π/8) + cos(7π/8) = 0
Advertisement
#SciPiTutor
#TrigonometricValue
#Trigonometry
#Mathematics




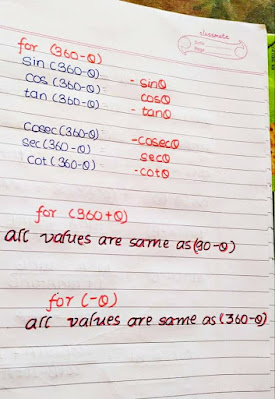

0 Comments