Prove geometrically the Trigonometric values of sin, cos, and tan at 30°.
Values of Trigonometric Ratios are easier to understand if memorized. But, imagine someone asks you to derive these formulae using a diagram! Won't you be ashamed of yourself for not knowing the solution?
Wait not anymore! Check this geometrical proof of trigonometric ratios at 30°.
Answer:
Take an equilateral triangle to help you with this solution.
Remember in an equilateral triangle,
All the sides are equal to each other. All angles are 60°.
Is it hard for you to understand that <BAD and <CAD are equal?
Well, that's because any vertical line if drawn perpendicular to the base of either isosceles or equilateral triangle from the vertex divides the vertical angle into two equal angles and cuts the base into two equal parts.
From this, we can say: <BAD = <CAD and BD = CD.
Pythagoras theorem states that, "the sum of the squares of the perpendicular and the base of a right angled triangle is equal to the square of its hypotenuse."
This means,
h²=p²+b²
Or, p² = h² - b²
Click here to learn more about: Values of Trigonometric Ratios
This is how we can prove the Trigonometric values of all six Trigonometric Ratios.
Cosec x = h/p
Sec x = h/b
Cot x= b/p
Check these related notes:

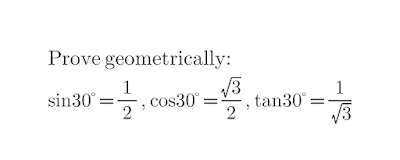







0 Comments