Sample Questions and Solutions
Subject: Optional Mathematics. Class: 9
You may be searching for: Trigonometry Class 9 Solutions. Click here.
Group A
1. a) Define the range of a function.
1. b) Find the third term of the series:

2. a) Write x→-7 in a mathematical sentence.
2. b) Write the formula to find the area of a triangle.
3. a) Find the slope of the line, y= 6x + 7.
3. b) Find x-intercept and y-intercept in the line: $\dfrac{x}{4} +
\dfrac{y}{5} = 1$
4. a) Write the formula of Trigonometric ratio of sin(270° - A)
4. b) Find the value of:
5. a) If the position vector of A and B are (a,b) and (c,d) respectively,
find the column vector of vector 'AB'.
5. b) Write down the image of point P(x,y), when it is rotated under -90°.
Group B
6. a) If (2x, 2x+3y) and (x+4,20) are equal order pairs, find the value of x
and y.
6. b) If the polynomials f(x) = x³ +(m+2)x² +x +3 and g(x) = x³ +4x² +(n-1)x
+3 are equal.Findd the value of m and n.
6. c) If Sn = n²+ 1, then find tn.
7. a)
8. a) The given points (-5,1) , (5,5) and (k,7) are collinear Find the value
of k
8. b) Find the value of 'k' so that the point (-3,2) lies on locus:
x²+y² -ky -21 = 0
8. c) Prove that: Vector AB+ Vector BC = 2 Vector AM, where M is midpoint of
BC.
9. a) In the figure, if HG= 4 units and <HGF = 30°, Find the equation of
AB.
b) Find the value of secA, if tanA= ¾.
10. a) In a discrete data, Σ fx= 2400, N = 100 and Σf(x -x̄) = 448, then find the mean deviation from mean and it's coefficient.
b) Vector PQ displaces P(3,4) to Q(-1,1), find the direction of Vector PQ.
Advertisement
Group C
11. If two functions are f(x) = x² -3x +2 and g(x) = x³ -6x²
+x+1 are given, find the product of f(x)*g(x). Also find the degree of the
product.
12. If I is an Identity matrix of order 2×2 and O is a null matrix of
order 0×0. Verify that: OI = IO= O.
13. If Sn = n²+ n. Find S4, S5 and
t5.
14. Calculate the limit of:
15. Find the equation of a straight line passing through the points
(-1,3) and making equal intercepts on coordinate axes.
16. If A,B,C and D are four points with co-ordinates (6,3) , (-3,5) ,
(4,-2) and (a,3a) respectively.
17. If secA + tanA = x, then show that:
18. Find the value of x:
xsec(90+ A). CosecA + tan(90+ A). Cot(180- A) = xcotA.tan(90+ A)
19. Rotate the quadrilateral with vertices E(2,0) , F(4,0) , G(2,3)
and H(4,5) under -270° turn about origin. Write the coordinates of the image
and plot object and image on the same graph.
20. Calculate the quartile deviation and coefficient.
21. Calculate the Standard deviation from the given data and
it's coefficient.
Group D
22.Find the coordinate of the point which divides
internally, the line joining two points (x1, y1) and (x2, y2) in the given
ratio m:n.
23. Find the point of trisection of the line segment joining
the points (1,-2) and (-3,4).
24. P and Q are two points with co-ordinates (-1,3) and
(4,2) respectively, find
I. Vector PQ
II. Direction of vector PQ
III. Unit vector along with direction of vector PQ
25. A(2,2) , B(5,2), C(8,4) , and D(1,4) are the vertices of
trapezium. Find the image under enlargement with center at (4,-1) and scale
factor 2.
________________________________________________
Answers:
Answer 1 a)
Range of a function can be defined as the set of all the elements of SetB
which are the images of Set A in the given function f : A → B.
Answer 1 b)
We have, nth term = 2n +4
When n= 3
t3 = 2×3 +4
= 10
Hence, the third term of the series is 10.
Answer 2 a)
According to the question, the mathematical statement would be x 'tends to'
-7 or x 'approaches to' -7.
Answer 2 b)
Formula to find the area of a triangle is:
Area =
Answer 3 a)
Comparing the given equation y=6x+7 with y=mx+c,
We have, m=6
Therefore, the slope of the given line is 6.
Answer 3 b)
Comparing the formula with double intercept formula we get,
x-intercept= 4
y-intercept= 5
Answer 4 a)
Formula of Trigonometric ratio: sin(270°-A) is (-cosA.)
Answer 4 b)
We know π=180°
Sec Π/3
= Sec 180°/3
= Sec 60°
= 2
Answer 5 a)
Answer 5 b)
Rotation under -90°
P(x,y) -------------> P(y,-x)
Answer 6 a)
From the relation of equal ordered pairs,
We have,
2x = x+4
or, 2x -x= 4
Therefore, x= 4
And, 2x+ 3y= 20
or, 2×4 + 3y = 20
or, 8 + 3y = 20
or, 3y = 20-8
or, 3y = 12
or, y= 12/3
Therefore, y= 4
So, (x,y) = (4,4)
Answer 6 b)
From the relation of equal polynomials,
Coefficient of equal terms are also equal.
So,(m+2)x² = 4x²
or, m+2 = 4
or, m = 4-2
Therefore, m= 2
And,
x= (n-1)x
or, 1 = n-1
or, 1+1 = n
Therefore, n= 2
So, m= n= 2
Answer 6 c)
Given,
Sn = n²+ 1
Sn-1 = (n-1)²+ 1
= n²-2n +1 +1
= n² - 2n + 2
We know,
tn = Sn - Sn-1
= n²+ 1 - (n² - 2n + 2)
= n² + 1 - n² + 2n - 2
= 2n - 1
Answer 7 a)
Given,
From the relation of equal matrices,
a+b = 6
or, a= 6-b
And,
ab = 8
or, (6-b)b = 8 [Putting the value of a =6-b]
or, 6b -b² = 8
or, 0 = b²-6b +8
or, b²-6b +8 = 0
or, b² -(4+2)b +8 =0
or, b² -4b -2b +8 = 0
or, b(b-4) -2(b-4) = 0
or, (b-2) (b-4) = 0
Either
b -2 = 0
So, b = 2
Or,
b-4 = 0
So, b= 4
Taking b=2,
a= 6-b
= 6 -2
= 4
Taking b=4,
a= 6- b
= 6-4
= 2
So, either (a,b) = (2,4)
Or, (a,b) = (4,2)
Answer 7 b)
Given, We had a small editing mistake: Matrix should always be represented
in big brackets! It has no meaning if it is represented in parentheses or
curly brackets.
Answer 7 c)
Given,
Answer 8 a)
Give,
Points are A(-5,1) , B(5,5) and C(k,7)
We know,
Slopes of collinear points are equal.
Let A(-5,1) be x1, y1
Let B(5,5) be x2, y2
Slope(m) = (y2-y1)/ (x2-x1)
= (5-1)/ {(5-(-5)}
= 4/ {5+5}
= 4/10
= 2/5
And,
Let B(5,5) = x1,y1
Let C(k,7) = x2, y2
Slope(m) = 2/5
So,
Slope(m) = y2-y1/x2-x1
or, 2/5 = (7-5)/(k-5)
or, 2/5 = 2/(k-5)
or, 2*(k-5) = 5*2
or, 2k -10 = 10
or, 2k = 10+10
or, 2k = 20
or, k= 20/2
Therefore, k=10
So, the required value of k is 10.
Answer 8 b)
Given,
Point (-3,2), let the point be (x,y)
Equation: x²+y²-ky-21=0
or, (-3)² + (2)² - k(2) -21 = 0
or, 9 + 4 - 2k = 21
or, 13 - 2k = 21
or, 13-21 -2k = 0
or, -8 = 2k
or, -8/2 = k
or, -4 = k
Therefore, k = (-4) .
The required value of k for the given point to be on locus is -4.
Answer 8 c)
Given,
M is the midpoint of BC.
So, Vector BM = Vector MC
or, -Vector BM= Vector CM ...a
In triangle ABM
Vector AM = Vector AB + Vector BM ....1
In triangle AMC
Vector AM = Vector AC + Vector CM .....2
Now, adding 1 and 2, we get
Vector AM + Vector AM = Vector AB + Vector BM + Vector AC + Vector CM
or, 2 Vector AM = Vector AB + Vector AC + Vector BM - Vector BM. [from ...a]
So, 2 Vector AM = Vector AB + Vector AC
#proved
Answer 9 a)
Given,
GH = 4 units =p
<HGF = 30°
We know, α is the angle made by the line in positive direction of x-axis.
Here, α is 150°.
We know, equation of line in perpendicular form is, xcosα+ ysinα = p
or, x cos150° + y sin150° = 4
or, x cos(180° -30°) + y sin(180°-30°) = 4
or, x (-cos30°) + y sin30° = 4
or, x (-√3/2 ) + y (1/2) = 4
or, (-√3x / 2) + (y/2 )= 4
or, (-√3x + y)/2 = 4
or, -√3x + y = 4*2
or, -√3x + y = 8
or, √3x - y +8 = 0 is the required equation.
Answer 9 b)
We have tanA = ¾
SecA = √(1+tan²A)
= √{1+ (¾)²
= √ (25/15)
= √ (5/4)²
= 5/4
Answer 10 a)
We have,
Σ fx= 2400, N = 100 and Σf(x -x̄) = 448
Mean Deviation (M.D.) = Σf(x -x̄)/ N
= 448/100
= 4.48
Mean = Σ fx/N
= 2400/100
= 24
And coefficient of M.D. = M.D. / mean
= 4.48/24
= 0.187
Answer 10 b)
Answer 11)
Given,
f(x) = x² -3x +2 and g(x) = x³ -6x² +x+1
f(x)*g(x) = (x² -3x +2)( x³ -6x² +x+1)
= x²( x³ -6x² +x+1) -3x( x³ -6x² +x+1) +
2( x³ -6x² +x+1)
= x^5 -6x⁴ +x³ +x² -3x⁴ + 18x³ -3x² -3x +2x³ -12x² +2x +2
= x^5 -6x⁴ -3x⁴ +x³ +18x³ +2x³ +x² -3x² -12x² +2x +2
= x^5 -9x⁴ +21x³ -14x² +2x +2
And, degree of polynomial is 5.
Answer 12)
Answer 13)
Given,
Sn = n²+ n
When n= 4,
S4 = 4²+ 4
= 16+4
= 20
When n= 5,
S5 = 5²+ 5
= 25+5
= 30
When n= (n-1)
Sn-1 = (n-1)²+ (n-1)
= n²-2n +1 +n -1
= n² -n
Now,
tn = Sn - Sn-1
= n² + n -(n²-n)
= n² + n - n² + n
= 2n
And when n= 5 in tn
t5 = 2*5
=10
Therefore,
S4 = 20
S5 = 30
t5 = 10
Answer 14)
Given,
Answer 15)
Answer 16)
Advertisement
Answer 17)
Answer 18)
Answer 19)
Given,
Co-ordinates of the points are
E(2,0) , F(4,0) , G(2,3) and H(4,5)
Rotation under -270°
P(x,y) ------> P'(-y,x)
E(2,0) ------> E' (0,2)
F(4,0) ------> F' (0,4)
G(2,3) ------> G' (-3,2)
H(4,5) ------> H' (-5,4)
Therefore, the co-ordinates of the image are: E'(0,2) , F'(0,4) , G'(-3,2)
and H'(-5,4).
Therefore, the coordinates of the image and the object are plotted in the
graph above.
Answer 20)
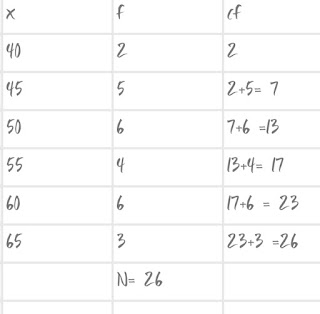
Arranging the given data in ascending order,
Q1 = [ (N+1) /4 ] th item
= [ (26+1)/4 ] th item
= [ 27/4 ] th item
= 6.75 th item.
In cf table, just greater value than 6.75 is 7 whose corresponding value is
45. So, Q1= 45
Q3 = 3 [ (N +1)/4 ] th item
= 3 [6.75 ] th item
= 20.25 th item
In cf table, just greater value than 20.25 is 23 whose corresponding value
is 60. So, Q3 = 60
Now, Quartile Deviation = (Q3 - Q1)/ 2
=(60-45)/2
= 15/2
= 7.5
And, Coefficient of Quartile Deviation =
(Q3-Q1)/(Q3+Q1)
= (60-45)/(60+45)
= 0.14
Answer 21)
Given,
Answer 22)
Answer 23)
Given points are:
A(1,-2) and B(-3,4).
We know, when two points are trisected, they are internally divided in the
ratio m:n=1:2.
Let C be that point whose coordinates are (x,y)
Let A(1,-2) = (x1,y1) and B(-3,4)= (x2,y2)
Using section formula of internal division:
x= (mx2 + nx1)/(m+n)
= {1.(-3) +2.1} / (1+2)
= {-3 +2} /3
= -1/3
y= (my2+ my1)/(m+n)
= {1.4 + 2.(-2)}/ (1+2)
= {4 -4}/3
= 0/3
= 0
So, C(x,y)= (-1/3,0)
And, D is the midpoint of B and C
So,
Let B(-3,4)=(x1,y1) and C(-1/3, 0) = (x2,y2)
Let the coordinates of D be (x3,y3)
We have,
x3= (x1+x2)/2 = {(-3) + (-1/3)} /2
= {-3 -1/3}/2
= -10/6
= -5/3
y3 = (y1+y2)/2
= (4+0)/2
= 2
So, coordinates of D are (-5/3 , 2)
Therefore the points of trisection are C(-1/3,0) and (-5/3,2).
Answer 24)
Answer 25)
Given, coordinates of points of trapezium are:
A(2,2) , B(5,2), C(8,4) , and D(1,4)
Enlargement under center (a,b) (4,-1) and scale factor (k)=2,
P(x,y) ---------> P'2{x-4)+4, 2(y+1)-1}
A(2,2) ---------> A' (0,5)
B(5,2) ---------> B' (6, 5)
C(8,4) ---------> C'(12,9)
D(1,4) ---------> D'(-2,9)
So,the coordinates of the everyone's of the image of trapezium are A'(0,5),
B'(6,5) , C'(12,9) and D'(-2,9)
_________________________________________________
We hope we have been able to help you with all these questions. Make sure to
check out our other posts.
Follow us on facebook: @scipitutor
Sample paper class 9, optional mathematics, question paper with solutions,
guess paper 2020
#SciPiTutor
#OptionalMathematics
#SamplePaper































1 Comments
How to find quartiledeviation and it's coffecient
ReplyDelete