If sinA = 12/13 , find cosA and tanA.
This is question from the Values of Trigonometric Ratios chapter of Unit Trigonometry. You can find the solution in the picture and the brief explanation is given below the image. Here is the solution.
Answer:
This is one of the easiest question in Trigonometry!
When we have been given the value of sin A, to find cos A we just need to apply and solve the Trigonometric identity.
Here is further detailed solution:
Solution:
Given,
sinA = $\dfrac{12}{13}$
We know,
cosA = $\sqrt{1-sin^2A}$
= $\sqrt{1- \left ( \dfrac{12}{13} \right ) ^2}$
= $\sqrt{\dfrac{169-144}{169}}$
= $\sqrt{\dfrac{25}{169}}$
= $\dfrac{5}{13}$
Also,
tanA = $\dfrac{sinA}{cosA}$
= $\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}$
= $\dfrac{12}{5}$
Therefore, cosA = $\dfrac{5}{13}$ and sinA = $\dfrac{12}{5}$.
And then we can simply find the value of Trigonometric ratios in Trigonometry.
You can get more help by visiting these useful links:
Link: Compound Angles
Link: Values of Trigonometric Ratios
Link: Introduction To Trigonometry
#SciPiTutor
#TrigonometricValues
#Trigonometry
#Mathematics

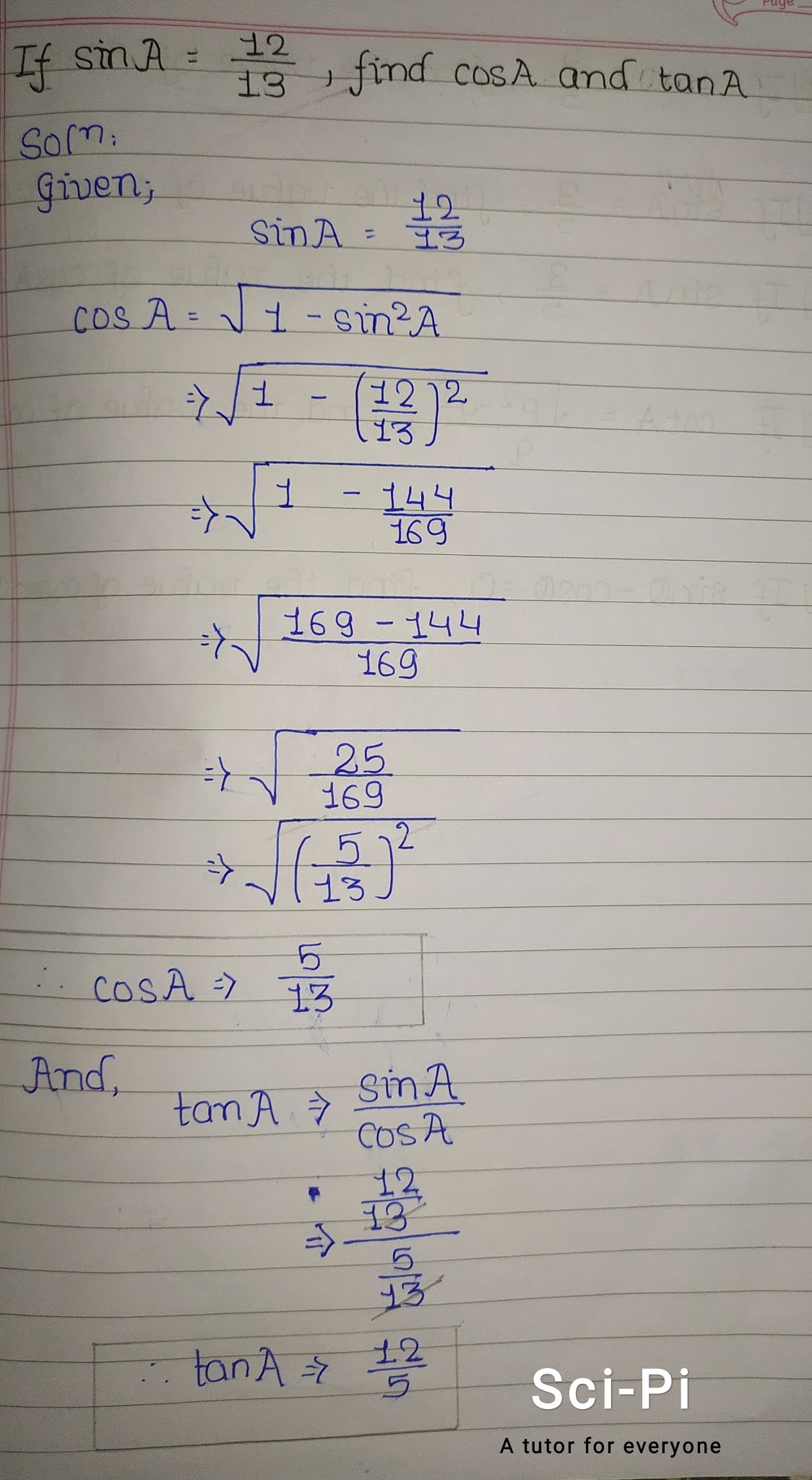

0 Comments