Overview: Matrix is the way of storing data, especially numbers in rectangular array, arranged in rows and columns format. Each data (number) in a matrix is called its element or entry. Every matrices are denoted by a capital letter. The size of the matrices is denoted by a small letter followed by two suffix. There are some special types of matrices.
Contents
In this notes, we will discuss about Matrix Class 9th notes, figure of matrix, notation of matrix, order or size of matrix, special types of matrix that are: row matrix, column matrix, square matrix, rectangular matrix, diagonal matrix, zero or null matrix, unit or identity matrix, scalar matrix, triangular matrix and few additional things.
Introduction to Matrix:
Storing data and keeping records in real life is essential. We might store them in different forms.
Matrix is the way of storing data, especially numbers in rectangular array, arranged in rows and columns format. Each data (number) in a matrix is called its element or entry.
Advertisement
Notation of Matrices (singular: Matrix):
Here are the important things to remember during notation of Matrices:
- Matrices are always denoted by capital letter.
- Elements or entries of any matrix are denoted by small letter. The letter should be the same used to denoted the respective matrix.
- The elements are further denoted by double suffix format, on the basis of their position in the matrix.
Let us take an example of matrix:
Here, the matrix is denoted by a capital letter 'A'.
So, we call this matrix as matrix A.
Now, we need to notate the elements of this matrix. For this, we will first use the same letter we used to denoted the matrix i.e. 'A'.
We know that, elements of the matrix are denoted by small letters. So, it will be 'a'. Also, they are denoted by double suffix.
The suffix are written by analysing the rows and columns. In the suffix, first number denoted rows and the second number denoted the column.
Rows are the horizontal line where columns are the vertical line.
In the above matrix, to notate element 3, we would write 'a12'. This is because the element 3 lies on the first row and second column.
Similarly, to denoted 6, we would write 'a23'.
For 4, 'a22' and so on.
Let us notate the above matrix 'A'. Here is the answer:
Order or size of the matrix:
While writing the order or size of the matrix, we write the total number of rows and columns in suffix. While, the matrix is denoted by the Capital letter.
Writing the order of the above matrix would be A2x3.
So, things to remember:
- Use the same capital letter that you used to denoted the matrix.
- Count the total number of rows and columns. Then, write them in suffix with 'x' (by sign) in the middle.
- Rows (also denoted by i) are written before the 'x' sign and columns (also denoted by j) are written after the 'x' sign.
Some people may be confused with notation of elements matrix and order of the matrix because they are pretty much the same. Remember, in notation of elements of matrix, small letters are used. In order of matrix, capital letters are used with a 'x' sign in between of the two suffix.
Special Types of Matrices:
a) Row Matrix:
Row Matrix is that type of matrix in which the entries are arranged in only one row and more than one columns.
 |
| 1x2 row matrix |
 |
| 1x3 row matrix |
b) Column Matrix:
Column Matrix is that type of matrix in which entries are arranged in only one columns and more than one rows.
 |
| 2x1 column matrix |
 |
| 3x1 column matrix |
c) Square Matrix:
Square Matrix is that type of matrix in which data are arranged in equal number of rows and columns.
 |
| 2x2 square matrix |
 |
| 3x3 square matrix |
d) Rectangular Matrix:
Rectangular Matrix is that type of matrix in which data are arranged in unequal number of rows and columns.
 |
| 2x3 rectangular matrix |
 |
| 3x2 rectangular matrix |
e) Null or Zero Matrix:
Null matrix is that type of matrix, either square or rectangular, having all of its elements equal to zero.
 |
| 2x2 Null Matrix |
 |
| 3x3 Null Matrix |
f) Diagonal Matrix:
Diagonal Matrix is a type of square matrix whose elements other than the principal diagonal are equal to zero.
 |
| 3x3 Diagonal Matrix |
g) Scalar Matrix:
Scalar Matrix is a type of diagonal matrix whose all elements on the principal diagonal are the same number.
 |
| 2x2 scalar matrix |
 |
| 3x3 scalar matrix |
Advertisement
h) Unit Matrix or Identity Matrix:
Identity matrix is a type of diagonal matrix whose all elements on the principal diagonal are unit (1).
 |
| 2x2 Identity Matrix |
 |
| 3x3 Identity Matrix |
i) Equal Matrices:
Equal Matrices is the condition where two matrices have the same orders and their corresponding entries (elements) are also same.
 |
| Matrix A = Matrix B |
j) Symmetric Matrix:
Symmetric Matrix is a type of matrix that fulfills the condition aij = aji for all values of i and j.
 |
| 2x2 Symmetric Matrix |
k) Triangular Matrix:
Triangular Matrix is that type of matrix in which either the elements above or below the principal diagonal are zero.
In triangular matrix, we have two types of matrices:
i) Upper Triangular Matrix: If the matrix has all its elements below the principal diagonal equal to zero, it is said to be upper triangular matrix.
 |
| Upper Triangular Matrix |
ii) Lower Triangular Matrix: If the matrix has all its elements above the principal diagonal equal to zero, it is said to be lower triangular matrix.
 |
| Lower Triangular Matrix |
This is much for today's notes on Part 1 of Matrix for class 9. On part 2, we will discuss how to perform operations on Matrices and their properties.
#SciPiTutor
#Class9
#OptionalMathematics
#Matrix


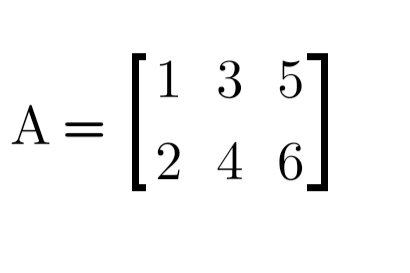


0 Comments