Contents
Mensuration:
Mensuration is the basic part of geometry related with finding the perimeter, areas and volumes of the objects.
In this chapter, we will have an overview of the Formulae of Area and Perimeter of Some Basic Plane Surfaces. And, derivation of Formulae of the Area of a Triangle.
Perimeter:
Perimeter is the sum of all the sides of a plane figure.
Area:
Area is the total surface occupied by any body.
Things to remember:
- The unit of perimeter is written same as the unit of length as perimeter is just the addition of all sides of a plane figure.
- The unit of area is written as square unit.
1. Triangle:
A triangle is a plane figure having three sides.
Area = 1/2 * b * h
Perimeter = a +b +c
2. Rectangle:
A rectangle is a plane figure having four sides, each opposite sides are equal and parallel to each other.
Area = l * b
Perimeter = 2 (l +b)
3. Square:
A square is a plane figure having four equal and parallel sides and all angles are 90°.
Area = l²
Perimeter = 4l
Advertisement
4. Parallelogram:
A parallelogram is a quadrilateral whose opposite sides are parallel and equal to each other but angles are not 90°.
Area = b *h
Perimeter = 2(l +b)
5. Rhombus:
A rhombus is a quadrilateral having all sides equal but not all angles are equal.
Area = 1/2 * d1 * d2
Perimeter = 4a
6. Trapezium:
A Trapezium is a quadrilateral having one pair of sides parallel to each other but not equal.
Area = 1/2 * h(l1 +l2)
Perimeter = a + b + c +d
7. Kite:
A Kite is a quadrilateral having two corresponding sides equal to each other.
Area = 1/2 *d1 *d2
Perimeter = 2(a +b)
8. Quadrilateral:
A plane two-dimensional figure having four sides is said to be a quadrilateral.
Area = 1/2 *d (p1 +p2)
Perimeter = a +b +c +d
Advertisement
Area of a Triangle:
Triangles can be divided into three types on the basis of sides. If all the sides of a triangle are equal, that triangle is said to be an equilateral triangle. If two of the sides of a triangle are equal, that triangle is said to be an isosceles triangle. If none of the sides of a triangle are equal, that triangle is said to be a scalene triangle.
Triangle can also be divided into three types on the basis of angles. If all the angles of a triangle are less than 90°, that triangle is said to be an acute-angled triangle. If one of the angles of a triangle is equal to 90°, that triangle is said to be a right-angled triangle. If any one of the angle of a triangle is greater than 90°, that triangle is said to be an obtuse-angled triangle.
There are so many formulae to find the Area of a Triangle. Here, we have the formuale of area of the following triangles:
1. Area of a triangle in terms of its base and height:
In general cases, we will have the following figure of the triangles.
In such cases, to find the area of the triangle, we need to know the values of 'h' (that represents the height of the triangle) and 'b' (that represents the base of the triangle). Then we can use the following formula:
2. Area of a right-angled triangle:
A triangle having one angle equal to 90° is said to be a right-angled triangle.
In such cases, we need to know the values of 'p' (that represents the perpendicular height of the triangle) and 'b' (that represents the base of the triangle). Then, we can use the following formula to evaluate its area:
3. Area of an equilateral triangle:
A triangle having all of its side equal is said to be an equilateral triangle. Let us represent the sides of the equilateral triangle by 'a'. Then, we get the following figure:
As we know, the line joining the vertex of an isosceles triangle and perpendicular to its base, bisects the base.
So, our base can be divided into 'a/2' each, as shown in the figure.
Using Pythagoras Theorem,
AD = √(AB² -BD²)
= √{a² - (a/2)²}
= √{(4a²-a²)/4}
= √{3a²/4}
= √3/2 a
We have,
Base of the triangle (b) = BC = a
Height of the triangle (h) = AD = √3/2 a
Now,
Putting the values in the general formula of area of triangle, we get;
A = 1/2 * b * h
= 1/2 * a * √3/2 a
= √3/4 a²
And, we get the following formula:
Advertisement
4. Area of an isosceles triangle:
A triangle having two of its side equal is said to be an isosceles triangle.
Let the two equal sides of the triangle be 'a' and the third unequal side be 'b'. Then,
Using the statement of Isosceles triangle, we get, BD = CD = b/2
Using Pythagoras Theorem,
AD = √(AB² -BD²)
= √{a² - (b/2)²}
= √a² - b²/4
= √(4a²-b²)/4)
= √(4a²-b²)/2
We have,
Base of the triangle (b) = BC = b
Height of the triangle (h) = AD = √(4a²-b²)/2
Now,
Putting the values in the general formula of area of triangle, we get;
A = 1/2 * b * h
= 1/2 * b * √(4a²-b²)/2
= 1/4 * b * √(4a²-b²)
And, we get the following formula:
5. Area of a scalene triangle:
A triangle having none of its side equal is said to be a scalene triangle.
Let, one side of the triangle be 'a', another side be 'b' and the remaining side be 'c'. Then,
Let '2s' represent the perimeter of a triangle, then,
2s = a+b+c
or, s = (a+b+c)/2
The equation [s = (a+b+c)/2] represent the semi-perimeter
of a triangle.
In right-angled triangle ADC,
Using Pythagoras Theorem,
AD² = AC² -DC²
or, h² = b² -x² -----(i)
And,
In right-angled triangle ABD,
Using Pythagoras Theorem,
AD² = AB² -BD²
or, h² = c² - (a-x)² -----(ii)
From equations (i) and (ii), we get;
b² -x² = c² -(a-x)²
or, b² -x² = c² - a² +2ax -x²
or, b² -x² -c² +x² +a² = 2ax
or, 2ax = a²+b² -c²
or, x = (a²+b²-c²)/2a ----(iii)
From equations (i) and (iii), we get;
h² = b² - {(a²+b²-c²)/2a}²
= [b - {(a²+b²-c²)/2a}] [b + {(a²+b²-c²)/2a}]
= {(2ab -a²-b²+c²)/2a} {(2ab +a²+b²-c²)/2a}
= [{c² -(a-b)²}/2a] [{(a+b)² -c²}/2a]
= [(c+a-b)(c-a+b)/2a] [(a+b+c)(a+b-c)/2a]
= [(a+b+c-2b)(a+b+c-2a) (a+b+c)(a+b+c-2c)]/4a²
Now, substituting, a+b+c = 2s, we get,
h² =[ 2s(2s-2c) (2s-2b) (2s-2a)]/4a²
= [16s (s-a)(s-b)(s-c)]/ 4a²
or, h = 2/a √(s(s-a)(s-b)(s-c)
Now,
Putting the values in the general formula of area of triangle, we get;
A = 1/2 * b* h
= 1/2 * a * h
= 1/2 * 2/a √(s(s-a)(s-b)(s-c)
= √(s(s-a)(s-b)(s-c)
And, we get the following formula:
#SciPiTutor
#Class10
#Mensuration
#Mathematics















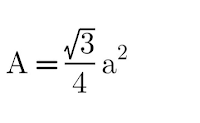





1 Comments
Please show me class 10 solution
ReplyDelete