Find the notes here:
5. Solution of a System of Linear Equations - Matrix Method
6. Cramer's Rule
Out of Syllabus
Overview: Matrix is the way of storing data, especially numbers in rectangular array, arranged in rows and columns format. Matrix allows us to solve the problems of linear equations. These can be solved using determinant, inverse of a matrix and cramer's rule. We will learn briefly about all these here in this notes.
Contents
To learn the basics of matrix, follow these links:
Determinant:
Determinant is defined only for square matrices. In a 2x2 square matrix, it is
a number calculated by subtracting the product of the other two elements (in
diagonal) from the product of the principal diagonal elements.
Determinant of a matrix is written as |A| or |A+B| or |B|. The name of the
matrix should be written inside '||'.
In a 1x1 square matrix, determinant is the same element in the matrix. i.e. A
= [a] and |A| = a.
Here is one solved example on determinant of 2x2 matrix:

|
Click here to learn the explanation of this solution.
Inverse Matrix:
In Inverse Matrix, we need to consider the following topics:
- Singular Matrix
- Non-Singular Matrix and
- Inverse Matrices
A square matrix is said to be a singular matrix if its determinant is
equal to 0.
A square matrix is said to be a non-singular matrix if its determinant
is not equal to 0.
Remember, Only inverse of a non-singular square matrix can be
calculated. Square singular matrix cannot have its inverse matrix.
Advertisement
Inverse Matrices, when multiplied give the product as Identity Matrix. Hence,
two non-singular square matrices, let 'A' and 'B' are said to be inverse
matrices if AB = BA = I, and all these matrices have the same order or size.
When A and B are inverse matrices, we can write:
A-1 = B
or, B-1 = A
The inverse matrix of matrix A of following order and elements can be found as
follows:
[To be updated] Click here to see
the process of finding the inverse of a matrix.
Solution Of A System Of Linear Equations:
Using the Inverse of Matrices and notating the linear equations in matrix
form, we can find the solution of the system of linear equation.
A linear equation is that equation which can be written in the form of
ax+by = c.
Let us take an example:
3x -3y = 6
5x +6y = -1
Using multiplication of matrices and relation of equal matrices, this system
can be written as follows:
Here, we get,
AX = B
If |A|≠ 0, we can find the inverse of matrix A.
So,
A-1 (AX) = A-1 B
or, (A-1 A)X = A-1 B
or, I X = A-1 B
or, X = A-1 B
Using this identity, we can solve the system linear equations.
[To be updated] Click here to see a solved example of Solution of a
system of Linear Equations.
Advertisement
Cramer's Rule:
Cramer's Rule is used to solve the system of linear equations in two variables
using determinants.
According to this rule,
When we have the following linear equations:
a1x +b1y = c1
And, a2x + b2y = c2
Here, x = ( c1b2 -c2b1) /
(a1b2 -a2b1)
And, y = ( a1c2 - a2c1) / (
a1b2 -a2b1)
While finding x and y, the denominators remain the same but the numerator are
different in each cases.
Let D1 = c1b2 -c2b1
And D2 = a1c2 - a2c1
Also D = a1b2 -a2b1
We can write: x = D1/D and y = D2/D
[To be updated] Click here to learn about derivation of formula of x
and y according to Cramer's rule.
[To be updated] See this example to know step by step explanation of
Cramer's rule and solution.
#SciPiTutor
#Class10
#OptionalMathematics
#Matrix



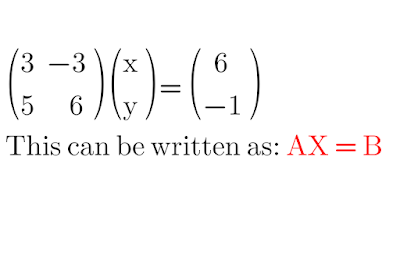

2 Comments
Put solution of a system of linear equation all exercise
ReplyDeleteVisit SciPiPupil for solutions!
Delete