Prove that: cos³A.cos3A +sin³A.sin3A = cos²2A | Trigonometric Identities of Multiple Angles | Sci-Pi (cos³acos3a+sin³asin3a = cos³2A)
This is a class 10 Question From Values of Trigonometric Ratios chapter of Unit Trigonometry (Multiples Angles).
Solution:
We know,
Our question is:
cos³A.cos3A +sin³A.sin3A = cos³2A
Taking LHS
cos³A.cos3A +sin³A.sin3A
[Put the values from (i) and (ii)]
= 4cos⁶A - 3cos⁴A + 3sin⁴A -4sin⁶A
= 4cos⁶A -4sin⁶A - 3cos⁴A +3sin⁴A
= 4(cos⁶A -sin⁶A) -3(cos⁴A-sin⁴A)
[Put the value of (cos⁶A -sin⁶A) from (iii) ]
= 4(cos2A)(1 -cos²Asin²A) -3(cos⁴A-sin⁴A)
[Put the values of (cos⁴A-sin⁴A) from (iv) ]
= 4cos2A(1 -cos²Asin²A) -3(cos2A)
= 4cos2A -4cos2Acos²Asin²A -3cos2A
= 4cos2A - 3cos2A - 4cos2Acos²Asin²A
= cos2A - 4(cos²A-sin²A)cos²Asin²A
= cos2A - 4cos²Asin²A (cos²A -sin²A)
[Put value of - 4cos²Asin²A (cos²A -sin²A) from (v) ]
= cos2A - 3cos²Asin²A(cos2A) -cos²Asin²A(cos2A)
= cos2A - cos²Asin²A(cos2A) - 3cos²Asin²A(cos2A)
= cos2A (1 -cos²Asin²A) - 3cos²Asin²A(cos2A)
[ Put cos⁶A -sin⁶A instead of cos2A - cos2A (1 -cos²Asin²A) from (iii) ]
= cos⁶A -sin⁶A - 3cos²Asin²A(cos2A)
= (cos²A)³ - (sin²A)³ - 3cosAsinA(cos²A -sin²A)
[We know, (a-b)³ = a³-b³-3ab(a-b) ]
= (cos²A - sin²A)³
= (cos2A)³
= cos³2A
= RHS
#proved
This is a FAQ question that has very little solution present on the Internet. We hope that this detailed solution will help you solving this question.
Some other indentities used in this solution are:
a²-b² = (a+b)(a-b)
(a³-b³) = (a-b)(a²+ab+b²)
a²+b² = (a+b)² -2ab
cos²A -sin²A = cos2A
Class 10 Mathematics Notes
Class 10 Optional Mathematics Notes
Class 09 Optional Mathematics Notes
Class 09 Optional Mathematics Notes
Class 09 Science Notes
FAQs
#FAQ
#SciPi

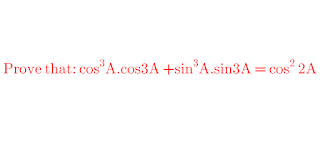

0 Comments